Числа редко вызывают восторг. Однако есть последовательность, которая будто скрыта в текстурах мира. Речь о последовательности Фибоначчи и связанной с ней «золотой» пропорции. Её ритм слышен в листьях подсолнуха, в очертаниях морской раковины, в фасадах храмов и в дизайне современных приложений. Фраза «пропорции Фибоначчи и закон Фибоначчи» встречается в популярных объяснениях нередко, но за ней стоит цельный математический сюжет, уходящий корнями в Средневековье и продолжающийся в лабораториях XXI века. Давайте разберёмся спокойно и последовательно: кто такой Фибоначчи, откуда берутся числа, как из них рождается «золотое» отношение и почему этот мотив так настойчиво проявляется в природе, искусстве и инженерии.
Кто такой Фибоначчи и откуда берётся последовательность
Леонардо из Пизы, более известный как Фибоначчи, жил в XIII веке. Он вырос в торговой семье и много путешествовал по Средиземноморью, где познакомился с арабской математической традицией. Именно он популяризировал в Европе позиционную десятичную запись чисел и ноль, что радикально упростило расчёты. Его книга Liber Abaci («Книга абака», 1202) стала поворотным моментом для европейской коммерции и науки.
В этой книге есть задача о кроликах. Условие простое, почти игровое: сколько пар кроликов получится через каждый месяц, если каждая взрослая пара даёт новую пару, а молодые становятся взрослыми через месяц? Модель идеализирована, но решение строит цепочку чисел: 1, 1, 2, 3, 5, 8, 13, 21… Каждое следующее — сумма двух предыдущих. Так рождается последовательность Фибоначчи. Она не только элегантна, но и удивительно плодородна с точки зрения идей. Уже здесь прячется знаменитая «золотая доля» — отношение соседних чисел стремится к постоянной величине приблизительно 1,6180339887… Её называют золотым сечением (φ).
Золотое сечение как предел роста
Отношение соседних членов последовательности Фибоначчи быстро стабилизируется. Например, 13/8 ≈ 1,625; 21/13 ≈ 1,615; 34/21 ≈ 1,619… Значения колеблются и всё ближе подходят к φ. Это происходит не случайно. Золотое сечение — корень квадратного уравнения φ² = φ + 1. Его можно описать бесконечной дробью, а ещё — бесконечной вложенной формулой. Интересно другое: φ — это «идеальная» пропорция самоподобия. Если разбить отрезок на две части так, чтобы целое относилось к большей части так же, как большая — к меньшей, получится именно φ. В этой идее чувствуется математическая поэзия: форма, которая «узнаёт» себя при масштабировании.
Что здесь называют «законом»
В популярной литературе встречается выражение «закон Фибоначчи». Обычно под ним понимают наблюдение, что многие структуры растут и организуются в соответствии с отношениями, приближающимися к φ, или с шаблонами, основанными на числах Фибоначчи. Сразу важная оговорка: это не строгий физический закон наподобие второго закона термодинамики. Скорее — устойчивый эмпирический мотив, который часто проявляется в системах, где идёт конкуренция за пространство, свет, ресурсы и где действует принцип оптимальности.
Как числа становятся линиями и поверхностями
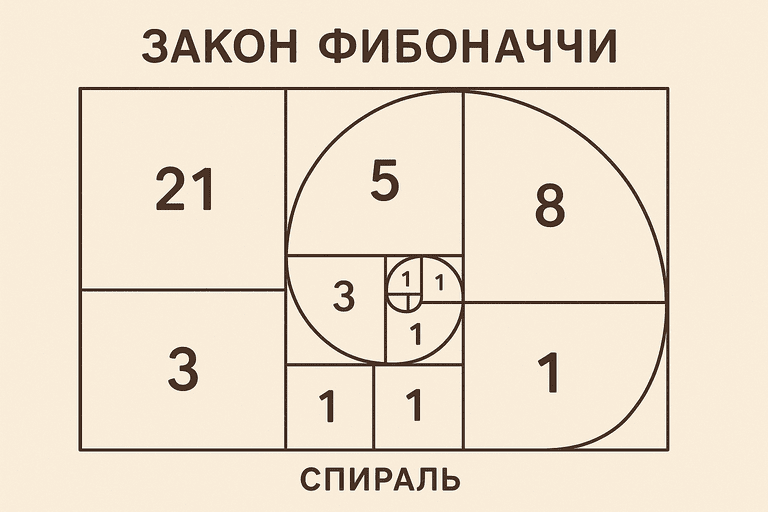
Числа сами по себе абстрактны. Однако из них легко собрать геометрию. Представьте прямоугольники, у которых стороны относятся как соседние числа Фибоначчи: 1×1, 1×2, 2×3, 3×5, 5×8 и так далее. Если из этих блоков составить каскад и дорисовать четверть окружности в каждом квадрате, получится спираль Фибоначчи — плавная линия, напоминающая естественные завитки. Она не совпадает идеально с логарифмической спиралью, где угловой шаг постоянен, но визуально очень близка. Именно поэтому многие популярные иллюстрации к «золотой пропорции» рисуют именно такую последовательность квадратов и дуг.
Кроме того, золотое сечение рождает золотой прямоугольник — фигуру, которая при разрезании на квадрат и прямоугольник даёт прямоугольник, подобный исходному. Этот эффект самоподобия важен для художника и архитектора: композиция может масштабироваться, сохраняя «мускулатуру» визуального баланса.
Природа и Фибоначчи: где совпадение, а где правило
Здесь легко уйти в мифологию, поэтому аккуратно отделим факты.
Во-первых, закономерный мотив — это филлотаксис, то есть закономерности расположения листьев, семян, чешуек на растениях. У подсолнуха, шишки или ананаса можно увидеть спиральные ряды в двух направлениях. Их количества часто — соседние числа Фибоначчи: 34 и 55, 55 и 89 и так далее. Это удобно для плотной упаковки элементов без пустот. Поэтому такая схема часто выигрывает у альтернатив.
Во-вторых, логарифмические спирали встречаются в природе повсеместно. Они описывают рост раковин моллюсков, рога некоторых животных, траектории циклонов. Спираль Фибоначчи — не точная формула этих линий, но она хорошее приближение, поэтому в популярной визуализации наблюдается смешение понятий. Главное помнить: природа не «знает» про прямоугольники 1×1 и 2×3. Ей «известны» принципы экономии энергии и оптимального распределения. Фибоначчиевы числа оказываются выигрышной стратегией в ряде случаев.
В-третьих, золотое сечение присутствует в биологических пропорциях. Иногда в его пользу приводят пример человеческого тела или лица. Здесь нужна осторожность. Статистические исследования дают неоднозначные результаты. У некоторых людей пропорции близки к φ, у многих — нет. Следовательно, это не универсальная «формула красоты», а один из приятных для глаза вариантов симметрии и баланса.

Искусство и архитектура: от Парфенона до плакатов
Искусство всегда искало гармонию. Поэтому золотое отношение стало удобным композиционным ориентиром.
Классическая архитектура. Часто говорят, что фасад Парфенона следует золотому сечению. Исследователи спорят: точные чертежи дают разные соотношения, а доказательств намеренного использования φ древними греками мало. Тем не менее визуально близкие пропорции действительно встречаются, потому что человеческому глазу комфортны умеренные отношения ширины и высоты — от 1,5 до 1,7.
Живопись и графика. Возрождение принесло интерес к измеримой красоте. Леонардо да Винчи и его современники активно изучали анатомию и геометрию. Хотя нельзя утверждать, что художники «повсеместно» чертили по φ, компоновка в районе золотых долей часто работает. Точка фокуса, смещённая примерно на 62% от края, выглядит естественно и динамично.
Современный дизайн. Афиши, интерфейсы, презентации — всё это выигрывает от иерархии и ритма. Золотой прямоугольник, сетки на основе последовательности (колонки шириной 1, 2, 3, 5, 8 условных единиц) дают чёткий порядок. Не нужно догматично прибивать макет к одной цифре, но полезно помнить: отношения соседних масштабов из Фибоначчи часто выглядят акустически «слаженно» и визуально «ровно».
Музыка: интервалы, формы и темп
Музыка не обошлась без этих чисел. Композиторы иногда строят структуру произведения так, чтобы кульминация приходилась примерно на золотое деление формы — около 0,618 от общей длительности. Это не правило, а выбор. Тем не менее приём работает: ожидание копится, и драматургический «вздох» звучит естественно.
В ритмике используют длины отрезков, кратные числам Фибоначчи, чтобы получить «живую» пульсацию. В электронике и киномузыке встречаются сетки 3-5-8-13 тактов. Кроме того, лады и аккордовые последовательности иногда проектируют с опорой на эти пропорции как на эвристику баланса. Никакой магии — просто естественная «шероховатость» вместо скучной симметрии 4-8-16.
Инженерия, данные и вычисления
В программировании числа Фибоначчи — не только романтика.
Алгоритмы. Существует поиск Фибоначчи и куча Фибоначчи. Первый — оптимизация поиска минимума на отрезке, второй — структура данных для эффективной работы с приоритетами. Идея проста: последовательность задаёт ступени разбиения или слияния, которые выгодны по сложности.
Сэмплирование и масштабирование. В визуализации данных удобно разносить уровни грануляции по шагам 1-2-3-5-8. Менеджер продукта часто делает так интуитивно: тарифы, колонки, карточки — всё складывается «лестницей» Фибоначчи и воспринимается предсказуемо.
Финансы. Технический анализ предлагает уровни коррекций 38,2%, 61,8% и расширения 161,8%. Эти проценты выводятся из φ и его степеней. Следует помнить: рынки — не растения, поэтому уровни — это инструменты психологии и референсы, а не гарантия движения цены. Они работают постольку, поскольку в них верит достаточно много участников.
Как применять пропорции Фибоначчи осмысленно
Слишком частое упоминание «золотой формулы» приводит к клише. Поэтому полезно придерживаться трёх принципов.
1) Ставить задачу, а не магическое число.
Нужно упаковать элементы без пустот? Подумайте о спиральных рядах и о плотности — здесь уместны паттерны, близкие к фибоначчиевым. Нужна визуальная иерархия? Примените сетку с шагами 1-2-3-5-8. Требуется точка фокуса? Проверьте, как смотрится деление около 0,62.
2) Проверять восприятие на людях.
Иногда макет по φ проигрывает простой трети. А порой равные колонки читаются лучше, чем «золотые». Следовательно, эксперимент важнее догмы. Тестируйте и оставляйте то, что работает для ваших пользователей.
3) Помнить об альтернативах.
Есть правило третей, диагонали, модульные сетки, пропорции корня из двух (≈1,414) и корня из трёх (≈1,732). Они тоже дают выразительные решения. Золотое сечение — мощный инструмент, но не единственный.
Расхожие мифы и аккуратные уточнения
Тема окружена легендами, поэтому разберём несколько популярных утверждений.
«Все великие произведения построены по φ». Нет. Многие — нет. Гармония многолика, и художники часто опираются на интуицию либо на другие схемы.
«Человеческое тело обязано подчиняться золотому сечению». Не обязано. Встречается близость к φ, но универсальности нет. Красота — не только в цифрах.
«Любая спираль в природе — спираль Фибоначчи». Чаще — логарифмическая, но с разными параметрами. Спираль Фибоначчи — наглядная учебная модель.
«Закон Фибоначчи» — физическая константа мира. Скорее — часто наблюдаемая закономерность оптимизации в условиях ограниченных ресурсов и роста.
Повседневные примеры, которые легко заметить
Смартфон и интерфейсы. Обратите внимание на карточки товаров: ширина, отступы, размер заголовков нередко подчинены ряду 8-13-21-34 пикселя. Дизайнеры делают так, чтобы глаз легко сканировал уровень за уровнем.
Фотография. Когда объект снимают не по центру, а смещают ближе к «золотой» точке кадра, сцена оживает. Это похоже на правило третей, только чуть «мягче».
Природа вокруг. Посмотрите на шишку сосны. Если провести спирали по рядам чешуек, получится пара чисел из последовательности. У подсолнуха история та же.
Музыкальные формы. Попытайтесь отследить, где «просыпается» трек — часто кульминация действительно приходит после середины, ближе к последней трети.
Почему это работает: короткая интуиция
Мир полон конкурирующих процессов. Листьям надо поймать свет, семенам — разместиться без пустот, интерфейсу — быть понятным без инструкции. Самоподобные и логарифмические схемы часто обеспечивают эффективность и предсказуемость роста. Числа Фибоначчи и золотое отношение оказываются удобным языком описания этих схем. Более того, человеческое восприятие любит мерную сложность: не хаос и не стерильную симметрию, а ритм с нюансами. Вот почему решения, «родственные» φ, кажутся нам естественными.
В чём ценность для читателя и создателя
Эта тема полезна не только математикам. Архитектор получает шаблон баланса, дизайнер — иерархию размеров, музыкант — опорные точки формы, фотограф — прикладываемую рамку, садовод — подсказку о природе спиральных ритмов, а инвестор — психологические уровни графиков (с оговорками). И, конечно, любой из нас может смотреть на мир внимательнее: там, где кажется случайность, порой таится стройность.
Числа Фибоначчи — это не заклинание и не секретный код вселенной. Это ясная и красивая модель роста, упаковки и восприятия. Она не объясняет всё, но помогает увидеть порядок среди множества вариантов. Стоит лишь один раз заметить, как из простого правила «следующее равно сумме двух предыдущих» возникает форма, ритм и образ, и вы уже иначе смотрите на подсолнечник, на постер в метро, на разворот журнала, на планировку комнаты, на мелодию в наушниках. В этом и есть сила: математика вдруг становится практикой внимания, а пропорции Фибоначчи и закон Фибоначчи — поводом слышать и видеть тонкую архитектуру повседневности.


